凯利公式：从博弈到投资的仓位管理智慧

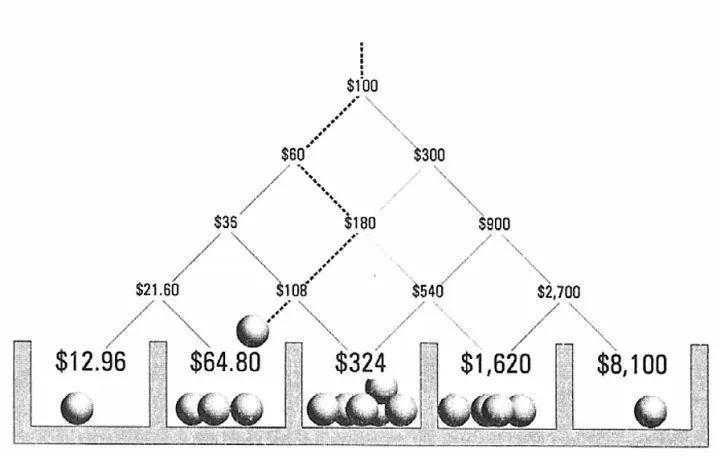
在金融市场与博弈领域，“如何合理分配资金、控制风险” 始终是核心命题。而凯利公式（Kelly Formula / Kelly Criterion）的出现，为这一问题提供了科学的数学解法 —— 它不仅是赌场中控制下注比例的 “安全准则”，更是投资市场里指导仓位分配的 “智慧工具”。​

凯利公式的起源可追溯至 1956 年，由美国贝尔实验室的约翰・凯利（John Kelly）提出。其核心思想并非追求单次收益最大化，而是在长期、重复的博弈中，通过找到最优资金比例，实现 “资金对数增长率最大化”。这一逻辑的关键在于：避免因过度重仓导致单次亏损击穿本金，也避免因过度轻仓浪费盈利机会，最终让资金曲线在长期维度上平稳向上。

在实际应用凯利公式时，需遵循清晰的步骤：第一步是 “数据收集与统计”，通过历史交易记录或策略回测，计算出准确的胜率​p和盈亏比​R—— 短期样本数据易受偶然因素影响，因此建议至少收集 50 次以上的完整交易记录，确保数据稳定性；第二步是 “公式代入与计算”，将统计好的​p和​R代入改写后的公式，得出理论最优仓位比例；第三步是 “实际仓位调整”，结合自身风险承受能力，对计算结果进行微调。​

值得注意的是，凯利公式并非 “万能工具”，实战中需警惕其局限性。首先，公式的理想化假设与现实存在差距 —— 它默认胜率和盈亏比是 “稳定不变” 的，但市场环境变化（如政策调整、行业周期波动）可能导致策略失效，原本的统计数据不再适用；其次，“全凯利下注”（即完全按照​f∗持仓）波动较大，极端行情下可能出现大幅回撤，因此多数专业投资者会选择 “半凯利”（​0.5f∗）或 “四分之一凯利”（​0.25f∗），以降低风险；最后，在多资产组合投资中，凯利公式需扩展为 “多资产凯利模型”，需考虑不同资产间的协方差（相关性），计算复杂度显著提升，普通投资者需借助专业工具辅助。​

归根结底，凯利公式的核心价值并非 “预测市场涨跌”，而是 “在已知策略有效性的前提下，合理分配资金”。它像一把 “精准的尺子”，帮助投资者在 “盈利空间” 与 “风险控制” 之间找到平衡点。在实际投资中，我们需理性看待其作用：既不忽视其科学逻辑，也不盲目迷信公式结果，始终结合市场动态、自身风险偏好调整策略，才能让凯利公式真正成为投资路上的 “助力”，而非 “桎梏”。